一、分治法时间复杂度计算
T(n)= aT(n/b)+ f(n) 展成树:则第二层的结点有a个,每个结点为f(n/b),所以整个第二层的和为a*f(n/b)。 这时三种情况: (1)a*f(n/b)和 f(n)是相等的,例如a=2,b=2,f(n)=n。那么说明每一层开销都是f(n)。而总共有logn层,所以T(n)=O(f(n)*logn)。 (2)a*f(n/b)比 f(n)小,例如a=2,b=3,f(n)=n。那么说明每一层都是递减的。这时候有一个技巧是可以直接把第一层f(n)当作T(n),即T(n)=O( f(n)) (3)a*f(n/b)比 f(n)大。那么这时候的技巧是T(n)=O(n^log以b为底的a),其他都不用考虑。 例如a=3,b=2,f(n)=n。每层增长是原来的3/2倍,所以总消耗是3/2的log以2为底的N的次方 * n= n^(log以2为底的3)。 注意:(1)如果是nlog(n/2)与nlog(n),我们当作相等来处理。情况1。一般的,对于nlog^k(n)类型的f(n)都做这样处理。注意2log(n/2)> 1log(n)。 (2)2/3 * n < n,情况2。 (3)3/2 * n > n,情况3。 (4)2 > 1,情况3。例如:T(n)= 2T(n/2)+ O(1),此时将1看成是n^0,所以a*f(n/b) = 2 *(1/2)^0 = 2。解出T(n)= O(n)。理解的关键是:(1)一定要将n的变化带入f(n)计算,而不是将f(n)整体加入计算。(2)整个树的和为T(n),当前一层都是确定的(加号后面的部分),下一层才是二分的不确定的部分。
二、随机二分查找一堆未排序数中第k大的数(quickselect)
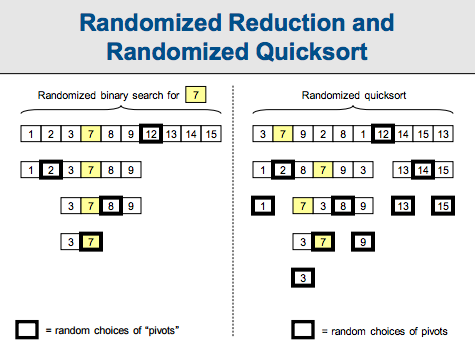
原理同快排。一轮处理pivot后,立即可以知道该pivot的排名r。因为比pivot低的排名已经全在pivot之前了,比pivot高排名的元素都在后面,r为pivot左边元素的个数。所以接下来就知道去哪边找第k大的数了。期望情况下,每次pivot都取到一半,那么时间复杂度公式为T(n)= T(n/2)+ O(n)=> T(n)=O(n)。在高概率的情况下,时间复杂度情况与快排相同,为O(nlogn),如下:
三、分治法查找一堆未排序数中的中位数
我们知道,查找一个未排序数组中的最大值和最小值,花费θ(n)的时间。因为只需一遍扫描即可知道。那么对于中位数呢? 分解为两个部分:第一个部分P1解决后,拥有它的中位数M1;第二部分P2解决后,拥有它的中位数M2 。那么我们可以知道总的中位数M一定介于M1和M2之间。反证法:如果M<M1<M2。根据中位数性质,P1中有1/2的元素比M1大,P2中有1/2的元素比M2大,相加起来发现会有总的1/2的元素比min(M1,M2)大,如果假设成立,那么会有1/2的数比M大,这与中位数的性质不符合,矛盾。同理,会有总的1/2的元素比max(M1,M2)小,M1<M2<M也不可能。 M介于M1和M2之间,这样问题缩小了一半。把介于M1和M2之间的元素过滤掉需要θ(n)的时间。 所以T(n)=2T(n/2)+ Θ(n)+T(n/2)=3T(n/2)+θ(n)。T(n)=O(n ^1.57).可见这种方法比先排序,然后取中位数的时间复杂度更大。 解决的方法是,分解为5个元素一组的子问题,所以有n/5个子问题。5个元素中发现中位数的时间复杂度为O(1),找到n/5组的中位数消耗θ(n)。然后在n/5个每组中位数中找他们中位数M‘消耗T(n/5)。M’的特点是什么呢?特点是它可以把所有数划分为比他小和大的两个部分:比他小的部分占3/5 * 1/2 = 3/10,比他大的部分占1 - 3/10 = 7/10。所以问题被缩小到7/10。 T(n)= T(n/5)+ T(7/10 *n)+ O(n)=> T(n)=θ(n)。 所以结论是:从一堆无序的数中找到中位数的代价是θ(n)。以后其他的算法(分治法中常常需要用中位数划分)中可以借用,只需要说明下有θ(n)时间找到中位数的方法即可。例如,快排中,如果借助该方法,每次找到中位数作为pivot,那么快排的时间复杂度将是θ(nlogn)。这种快排版本称为deterministic版本。
三、分治法求山峰最大视野间距
山峰视野间距是只被夹在某两个高峰之间的山峰(比两边都矮)的个数。 分治法:任意选择一个山峰做pivot,分解成了两边,变成两个子问题,然后加上计算从左边最高山峰和右边最高山峰之间的最大距离。结果取这三个子问题中的最大值。 其中从左边最高山峰到最右边最高山峰的距离一定要从两者之间矮的开始向高的方向找,找到第一个比自己高的。原因是如果从高向矮找第一个比自己矮的,那很可能过不了pivot,而从矮向高找一定能过pivot,因为矮的仍是所在边山峰中最高的。过不了pivot的情况被包含在了一侧的子问题中了,所以不可取。一定要取过pivot的情况。时间复杂度为O(n)。 总的时间复杂度为T(n)= 2T(n/2)+θ(n)= θ(nlogn)。
四、分治法求子数组最大和
数组中的元素可正可负,否则最大子数组之和就是整个数组之和。子数组是数组中一个滑动的窗口,不可以是间断的。 n个元素的子数组有n+(n-1)+(n-2)+…+1 种。 分治法以外的方法: (1)计算所有子数组之和:从第一个元素开始,计算以每个元素为起点的所有子数组的和,记录下最大值,随时看能否能更新。对一个元素开始计算所有子数组花费n^2,对所有元素计算一遍,总的复杂度为O(n^3)。如果利用前缀(prefix)数组来保存中间计算值,可以降到O(n^2)。 前缀数组P[j]= A[1]+ A[2]+…+ A[j]。所以在下标i和下标j之间的子数组窗口的和就等于P[j]- P[i-1]。 一旦花费n时间构建好p数组,接下来计算每个元素开始的所有子数组之和只需要n的时间复杂度了,总的时间复杂度下降到了O(n^2)。 (2)一种O(n)的方法:从第一个元素开始从左向右扫描,max记录当前最大值,sum记录当前窗口的和,如果每次sum小于0,则sum清0,表明使sum变零的这个窗口不选,如果max小于sum,则更新max。一遍扫描就可以得出子数组的最大和。 另一种O(n)的方法:计算出P[0]到P[i]需要O(n),对于下标j的最大子区间,就是找到0到j-1中最小的,用P[j]减去最小值。这样,只需在扫一遍就可以得出最大和。 分治法:任意一个元素为pivot,分解为两个子问题,加上包含该元素的中间子窗口。中间子窗口的计算为以该元素开始,向左一趟计算出最大值M1,向右一趟,计算出最大值M2,然后,中间子窗口的最大和就是M1+M2。最大和为三个值中最大的。 T(n)=2T(n/2)+θ(n) = θ(nlogn)。
五、分治法求有序序列k个值右移n位置后的序列中的k
显然,该序列满足第一个元素和最后一个元素相等。 取中间的元素,如果该元素左右两边第一个元素都比第一个元素小,说明答案在左半边;如果左右两边第一个元素都比第一个元素大,说明答案在右半边。如果左边第一个元素比第一个元素大,右边元素比第一个元素小,那么找到了。二分搜索,O(logn)。